hace poco estaba pagando unas compras en una perfumería. sobre
el mostrador había unos botes de gel de baño que estaban promocionando, y que
se caían en cuanto alguien los rozaba.
le dije medio en broma a la cajera: “es que no están bien
diseñados. son demasiado altos y estrechos, y al ponerlos de pie están en
equilibrio inestable”. le hizo mucha gracia, y me dijo entre risas: “me ha
gustado eso del equilibrio inestable, me lo apunto! ya sabes, se caen porque
están en equilibrio inestable!”, decía dirigiéndose a un compañero suyo.
últimamente he estado pensando sobre ese tema. en un envase
que contiene un líquido -también sería aplicable a un sólido en polvo o grano-, existe
por un lado el centro de gravedad del envase, que se encuentra a la mitad de su
altura; y por otro lado, el centro de gravedad del líquido que contiene, que está
a la mitad del nivel de líquido en ese momento.
llamaremos H
mayúscula a la altura del envase, y h
minúscula a la altura del líquido. la primera es fija y la segunda es variable:
a medida que el recipiente se va vaciando, h
disminuye.
el centro de gravedad del conjunto envase-líquido será una
especie de media ponderada de sus respectivos centros de gravedad. y estará
ponderada por sus masas. llamaremos M
mayúscula a la masa del bote, y m
minúscula a la masa de su contenido.
supondremos que se trata de un bote cilíndrico de radio R y altura H. las paredes del bote las vamos a considerar de espesor
despreciable, y su masa la obtendremos como producto de su densidad superficial
por su área. a dicha densidad superficial la llamaremos ρs. por otro lado, la densidad del líquido, el cual sí
tiene tres dimensiones, la denotaremos como ρv.
la masa del líquido es igual a su densidad multiplicada por
su volumen. dicho volumen es el de un cilindro de radio R y altura h minúscula.
por otro lado, la masa del envase es igual al producto de su densidad
superficial por su área. ésta se obtiene como la suma del área lateral del
cilindro -radio R y altura H mayúscula- y las áreas de sus bases
inferior y superior.
sustituimos estas expresiones de las masas en la fórmula
para hallar el centro de gravedad que veíamos un poco más arriba. simplificamos
dividiendo por π·R2 en el
numerador y en el denominador, y obtenemos una nueva expresión para el centro
de gravedad en función de las densidades, las alturas y el radio.
tantas letras pueden confundirnos un poco. vamos a dar
valores numéricos a la densidad superficial ρs del envase, a la densidad volumétrica ρv del líquido, al radio R del envase y a su altura H mayúscula. en cambio la altura h minúscula del líquido la dejamos
libre, ya que varía a medida que nuestro recipiente de lo que sea que contenga se
va vaciando.
y a continuación sustituimos esos datos en nuestra expresión
para el centro de gravedad.
ahora vamos a comentar un fenómeno curioso: a medida que el envase
se va vaciando, el centro de gravedad del conjunto envase-líquido va
descendiendo. da igual que consideremos que está ‘medio lleno’ o ‘medio vacío’,
lo cierto es que en su parte inferior hay líquido y en su parte superior sólo
hay aire.
en consecuencia, el centro de gravedad estará más
abajo, y por ello nuestro bote será más estable y resultará más difícil volcarlo.
pero esto tiene un límite. si el bote se sigue vaciando, el
centro de gravedad volverá a ascender. porque llegará un momento en que el poco
líquido que quede pesará menos que el envase. y el centro de gravedad del
envase vacío está a la mitad de la altura del mismo, como explicábamos al
principio.
dónde se encuentra el nivel de líquido para el cual el centro de gravedad
alcanza su mínimo de altura, y a partir de ese momento asciende de nuevo? para hallarlo
debemos derivar la expresión del centro de gravedad respecto a su variable, la
altura h del líquido en cada
momento.
una vez calculada la derivada del centro de gravedad respecto a h, la
igualamos a cero. esto nos conduce a una ecuación de segundo grado, de la que se
obtienen dos soluciones. descartamos la solución negativa y llegamos a la
siguiente conclusión...
en un recipiente cilíndrico de densidad superficial 0,1 g/cm2
-presumiblemente de plástico-, de altura 20 cm y diámetro 5 cm, lleno de un
líquido de densidad volumétrica 1 g/cm3 -igual a la del agua-, el nivel de
líquido que hace que el centro de gravedad se encuentre lo más bajo posible es
de 4,46 cm. algo menos de la cuarta parte de la altura del recipiente. parece un resultado bastante realista, no?
hace un par de meses subí a facebook un breve video en el
que hablaba de los centros de gravedad. no he sido capaz de descargarlo e
insertarlo, así que os lo enlazo aquí. he subido desde mi móvil más videos
chorras parecidos. éste no es de los mejores, pero está relacionado con el tema
de esta entrada. así me ponéis voz. ;)








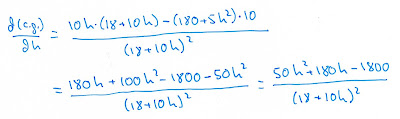

El vídeo del prisma ya me había gustado mucho en su día!!!!
ResponderEliminarQué pena que vivas tan lejos y que no te conocí antes porque lo que mi hijo pequeño sufrió con las mates, la física, la geometría y cualquier cosa que llevase números si le hubieses dado clase tú se lo habría ahorrado.
La mayor es muy de números, de hecho es lo que estudia, pero a él no se le dan bien y además creo que no consiguieron motivarle. Yo le ayudé hasta 4º de ESO, le explicaba las ecuaciones de segundo grado a mi manera, los polinomios, los sistemas de dos ecuaciones con dos incógnitas...y aunque no le gustaba más o menos fuimos tirando pero en bachiller, que para colmo eligió el científico, lo pasó pero fatal, acabamos yendo a profes particulares porque era un suplicio y aunque al final aprobó ninguno explicaba como lo haces tú, el razonamiento es la base, a mí me da igual que me digan que 2 y 2 son 4 si no me lo demuestran. Parece bobo pero si te demuestran empíricamente algo se queda mejor, y la comparación de la caja de cereales, por ejemplo, o de los botes de gel es buenísima. Un besito y me gustan mucho estos post, son enriquecedores.
Eres especial explicando las mates, y tienes una curiosidad inagotable, sigue así Chema.
ResponderEliminargema, a mí también me gusta demostrar las cosas. a algunos alumnos puede 'impacientarles' un poco, pero les digo: "tú sólo fíjate en lo que yo hago. no es necesario que lo entiendas al 100%, sólo que captes la idea y veas que esta fórmula sale de algún sitio y tiene su lógica". algunos chic@s eligen bachillerato de ciencias porque se necesita para la carrera que quieren estudiar, pero luego lo pasan mal con las matemáticas y la física. y en los dos últimos cursos se dan cosas muy complicadas.
ResponderEliminarañoranza, se hace lo que se puede, jeje. hacía mucho que no publicaba una entrada de este estilo. la anterior era la de los regalos de reyes, y como he quedado un poco saturado de fiestas, pensé "vamos a pasar página". y ayer escribí esta entrada volviendo amis orígenes. ;)
besos!!
Debo confesar, que siempre odié las mates. Se me daban bastante mal y los profes que he ido teniendo no ayudaron mucho, ya me hubiera gustado un profe como tú. De hecho ahora en Psicología he tenido bastante estadística y bueno, he ido aprobándola no me quejo, pero me las he visto y deseado para sacarlas adelante.
ResponderEliminarMe encanta como explicas las cosas, que las entiendo hasta yo. Harás que terminen cayéndome bien ;-)
Gracias profe
Me ha gustado también el termino ese del "equilibrio inestable" jejeje
ResponderEliminarana, no te preocupes, la mayor parte de las seguidoras de este blog son poco amigas de las mates, jejeje. me gusta relacionarlas con cosas reales. hay temas como por ejemplo potencias y raíces, que los considero un poco 'los tornillos y tuercas de las matemáticas'. es necesario saber manejarlos, pero por sí solos no tienen ninguna aplicación directa, por lo que resultan más aburridos tanto para el profesor como para el alumno. la estadística es complicadilla, ole por ti si la has aprobado!!
ResponderEliminargeno, lo del equilibrio estable / inestable da mucho juego. recuerdo un problema de física que era de una especie de montaña rusa sobre la que subía y bajaba una bola. quizá me vaya un día al parque de atracciones a hacer fotos para ilustrar una posible entrada sobre los equlibrios y las energías potenciales, jeje.
Jajaaj que entrada tan curiosa, yo siempre odie las mates, besitos...
ResponderEliminarMe he leído la entrada enterita pero hay partes que escapan a mi entendimiento. Lo que sí sé es que el bote de champú se cae inevitablemente muchas de las veces que te duchas!
ResponderEliminarNo he podido ver tu video, supongo que porque no tengo facebook. Pero bueno, yo ya te he puesto voz.
Igual un día te animas y haces una entrada sobre tus rotuladores de colorines. Son parte importante de este blog ;P
Besos
Tu entrada de hoy ha sido una clase magistral de Física...si te hubiera tenido como profesor seguro que me habría encantado esa asignatura de la que no tengo muy buen recuerdo.
ResponderEliminarGracias por venir a tomar el té
Un Beso
¿Sabes que eres un buen profe? explicas todo con detalle, y ya me hubiera gustado a mí tenerte de profesor, seguro que me hubieran gustado más las matemáticas, y te imagino delante de una pizarra de las de tiza, no de las de ahora digitales, explicando estas fórmulas viviéndolo como siento lo vives, entregado a tu asignatura, como un brillante profesor. Por cierto ¿este año a cuántos alumnos das clases?
ResponderEliminarUn beso muy grande.
rosana, los colorines son parte importante de este blog y de mis clases!! hay días en los que tengo que explicar cosas muy complejas, y uso casi todos los de la caja, para diferenciar bien los conceptos y poner todo tipo de flechas y símbolos varios, jeje.
ResponderEliminarprincesa, ahora alguno de mis alumnos ya da física y química, pero con más parte de química, que a mí se me da un poco peor aunque para explicarla a ese nivel no hay problema. cuando tenga que dar física sí que nos vamos a divertir!!
maría, se hace lo que se puede, jeje. en las clases explico mucho las cosas, porque precisamente para eso estoy, para explicar lo que los profesores de los colegios no explican. este curso tengo cuatro alumn@s de momento. anoche precisamente soñé que explicaba algo en una pizarra, con la tiza. :D
besos!!
Jamás hubiera analizado el motivo de su inestabilidad... simplemente hubiera pensado que tiene una mala base. Disfrutas como nadie entre números y fórmulas..., me recuerdas a un viejo profesor que tuve en la E.G.B. Era pasión por las matemáticas.
ResponderEliminarMil besitos, Chema.
auroratris, lo de la base también es importante, en eso tienes razón. debe ser una base con una mínima superficie de contacto para que el bote o lo que sea se sostenga con cierta estabilidad. pero esa estabilidad también depende de dónde esté situado el centro de gravedad, cuanto más abajo más estable. por ejemplo, al moldear un jarrón, la base debe ser más gruesa que el resto. eso los alfareros seguro que lo saben mucho mejor que yo, jeje.
ResponderEliminarbesos mil!!
Hola: el ordenador en cualquier momento me falla. Creo que no tiene memoria para tantos archivos e imágenes... por eso no me deja ver vídeos. Tengo que solucionarlo pero prefiero leer que ver.... Con respecto a los botes y su equilibrio es todo un mundo apasionante. Diseñar bien el envase es esencial. Como siempre, nos dan una lección de matrícula de honor sobre el tema. Seguimos en contacto
ResponderEliminarmarta, es verdad, hay objetos que no están diseñados. me pregunto si no tendrán ingenieros en las empresas de fabricación. no te preocupes por no ver el video, era una tontería. algún día coincidiremos en alguna quedada bloguera y ya me pondrás voz y movimiento. :)
ResponderEliminar