hace poco he tenido que repasarme el tema de los diferentes
centros de los triángulos, para explicárselo a mi alumna de 1º e.s.o.
el baricentro de
un triángulo es el punto de corte de sus medianas. las medianas son las líneas
que unen cada vértice con el punto medio del lado opuesto. el baricentro es el
centro de gravedad de un triángulo. es decir, en una figura material de forma
triangular, su centro de gravedad coincidiría con su baricentro.
el incentro de un
triángulo es el punto de corte de las bisectrices de sus ángulos. el incentro
es el centro de la circunferencia inscrita en un triángulo. es decir, aquella
circunferencia que se encuentra en el interior del triángulo y que es tangente
a sus tres lados. una vez obtenido el incentro, se trazará una perpendicular a
cualquiera de los lados del triángulo. el punto de corte será el punto de
tangencia. teniendo el centro y un punto, queda definida la circunferencia
inscrita.
el circuncentro
de un triángulo es el punto de corte de las mediatrices de sus lados. el
circuncentro es el centro de la circunferencia circunscrita al triángulo:
aquella circunferencia exterior al triángulo que pasa por sus tres vértices. el
radio de la circunferencia circunscrita será la distancia del circuncentro a
cualquiera de los tres vértices del triángulo.
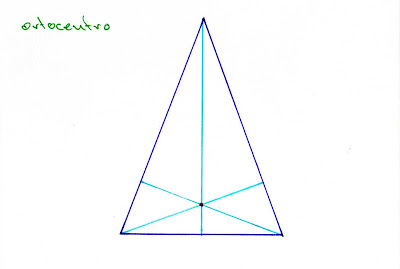
el ortocentro de
un triángulo es el punto de corte de sus alturas. las alturas son las líneas
perpendiculares a cada lado trazadas desde el vértice opuesto.
para hallar cualquiera de estos centros, basta con trazar
dos de las líneas que sean necesarias (medianas, bisectrices, mediatrices o
alturas) y determinar su punto de corte. si se traza la tercera restante y pasa
por el mismo punto, querrá decir que lo hemos hecho bien.
el baricentro y el incentro siempre se encuentran dentro del
área del triángulo, sea del tipo que sea. el circuncentro y el ortocentro sólo
se hallan dentro del triángulo para el caso de triángulos acutángulos. estos
triángulos son aquellos en los que sus tres ángulos son agudos (<90º).
veamos dónde quedan los cuatro centros para el caso de un
triángulo acutángulo escaleno. un triángulo escaleno es aquél en el que los
tres lados tienen diferente longitud.
en lo sucesivo, en las figuras correspondientes al incentro
y al circuncentro se representarán también la circunferencia inscrita y la
circunferencia circunscrita, respectivamente.
veamos ahora la representación de los centros y las
circunferencias correspondientes para un triángulo acutángulo isósceles. los
triángulos isósceles son aquellos en los que dos de los lados tienen la misma
longitud. y su particularidad en el tema que nos ocupa es que, para el vértice
opuesto al lado desigual, la mediana, la bisectriz, la mediatriz y la altura
coinciden.
queda un caso muy particular de los triángulos acutángulos,
y es el triángulo equilátero: sus tres lados y ángulos son iguales. en un
triángulo equilátero, las medianas, bisectrices, mediatrices y alturas
coinciden. y por tanto, también coincidirán en un único punto el baricentro, el
incentro, el circuncentro y el ortocentro.
aquí lo tenéis representado, con sus circunferencias
inscrita y circunscrita.
pasamos ahora a los triángulos rectángulos, que son aquellos
en los que uno de los ángulos es recto (=90º). en los triángulos rectángulos,
el circuncentro será un punto de la hipotenusa, y ésta será el diámetro de la
circunferencia circunscrita; y el ortocentro coincidirá con el vértice
correspondiente al ángulo recto, por coincidir dos de las alturas con los
catetos.
dentro de los triángulos rectángulos, veamos primero los
escalenos.
y ahora el caso del triángulo rectángulo isósceles: los dos
catetos son iguales. al coincidir la mediana, la bisectriz, la mediatriz y la
altura correspondientes al ángulo recto, la simetría será mayor.
quedan por analizar los triángulos obtusángulos, que son
aquellos que tienen un ángulo obtuso (>90º). en este tipo de triángulos, el
circuncentro quedará fuera del área del triángulo, “por debajo” del lado mayor,
tanto más cuanto más abierto sea el ángulo obtuso. y el ortocentro también
quedará fuera del triángulo, “por encima” del vértice correspondiente al ángulo
obtuso; más alejado cuanto más abierto sea dicho ángulo. para trazar las
alturas, prolongaremos imaginariamente los lados del triángulo cuando sea
necesario.
veamos primero el caso de los triángulos obtusos escalenos.
y ahora, los triángulos obtusángulos isósceles. en éstos, el
vértice correspondiente al ángulo obtuso, el punto medio del lado mayor, el
circuncentro y el ortocentro están alineados.
me resulta curioso que un punto que recibe el nombre de
‘centro’ quede fuera del área de la figura geométrica a la que pertenece. en el
caso de esos triángulos en los que su circuncentro y ortocentro quedan fuera de
su área, me imagino que están unidos al triángulo mediante hilos invisibles.