cuando se apilan objetos de sección circular, como puedan ser latas de conserva, inevitablemente quedarán huecos. este problema equivale al de llenar una superficie plana con circunferencias tangentes entre sí. siempre habrá resquicios que no se puedan ocupar.
vamos a comparar dos disposiciones diferentes que pueden
adoptar las circunferencias...
por un lado, se pueden colocar de tal manera que cada
circunferencia tenga cuatro ‘vecinas’ tangentes a ella: una a la derecha, otra
a la izquierda, otra encima y otra debajo. los centros de las circunferencias
superior, central e inferior están alineados, al igual que los de las
circunferencias izquierda, central y derecha.
se observa que las líneas que van uniendo los centros de
todas las circunferencias forman una red de celda cuadrada. el lado de dicho
cuadrado es igual al doble del radio de las circunferencias.
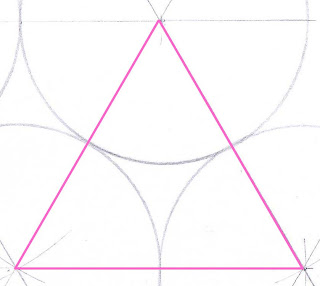
y por otro lado, se pueden disponer formando una estructura
similar a la del papel de burbujas. se colocan dos circunferencias tangentes
entre sí, y una tercera tangente a ambas. sus centros serán los vértices de un
triángulo equilátero. dicho triángulo será la celda unitaria de la red formada
al unir los centros de las circunferencias, y su lado será igual al doble del
radio de dichas circunferencias.
se intuye fácilmente que en esta estructura se aprovecha más
el espacio que en la anterior. los huecos son más pequeños, y además ahora cada
circunferencia tiene seis ‘vecinas’ tangentes a ella.
podemos calcular exactamente el porcentaje de
aprovechamiento del espacio en estas dos estructuras. para ello basta con
fijarnos en una celda unitaria, que es el patrón que se va repitiendo en las
dos direcciones del plano. el porcentaje obtenido se podrá extrapolar a toda la
red.
para el primer tipo de red, la celda es un cuadrado en cuyo
interior hay cuatro cuartos de círculo. llamaremos R al radio, y por tanto el
lado del cuadrado será 2·R.
el porcentaje de espacio lleno será igual al cociente entre
el área de esos cuatro cuartos de círculo y el área del cuadrado base, y todo
ello multiplicado por 100. el resultado es un 78.54%.
y para el otro tipo de red, la celda será un triángulo
equilátero que contiene tres sextas partes de un círculo. nuevamente llamamos R al
radio, y el lado del triángulo será el doble, 2·R.
el área del un triángulo, como sabemos, es igual a la mitad
del producto de su base por su altura. en un triángulo equilátero, la altura es
igual al lado multiplicado por el coseno de 30º, que es √3/2.
así, el porcentaje de espacio aprovechado será igual al área
de los tres sextos de círculo dividida entre el área del triángulo que los
contiene, y todo ello multiplicado por 100. obtenemos como resultado un 90.69%.
como vemos, el segundo tipo de estructura es mucho más
eficiente. y más estable desde el punto de vista físico. si intentáramos apilar
en una caja latas o botellas o cualquier objeto de sección circular de la
primera manera que hemos visto, tenderían a colocarse de la segunda manera,
acomodándose entre cada dos piezas circulares tangentes entre sí de la fila
inmediatamente inferior.
la estructura de red cuadrada, de hecho, es una situación de
equilibrio inestable. los centros de gravedad de las piezas apiladas se
encuentran en su posición más alta. la energía potencial es máxima.
todo lo contrario que en la red triangular, en la cual la energía potencial es
mínima al encontrarse los centros de gravedad en la posición más baja.
es lo que se denomina un equilibrio estable.
y cuando son botellas lo que estamos apilando, estas
consideraciones hay que tenerlas muy presentes, para que no se nos rompan!







Hasta ahora no me había fijado en como apilaba las latas pero no es tarde para aprender, sin duda la geometría tiene más aplicaciones de las que imaginaba más que nada porque no suelo pensar en ello así que me gusta que estés aquí para enseñarnos. La segunda de las formas es mucho más eficaz teniendo en cuenta lo escaso que suele ser, hoy día, el espacio de almacenamiento.
ResponderEliminarUn beso.
Chema, eres mi gurú de las mates! Me encanta el fin práctico que das a tus entradas teóricas.
ResponderEliminarwendy, habrás reconocido las viñetas de tintín, que tú también eres fan! buscaba alguna viñeta para hacer este post más ameno, y me acordé de estas dos de 'el cangrejo de las pinzas de oro'. a tintín le apresan en un barco, y en la bodega encuentra esa mercancía. en cuanto al aprovechamiento del espacio, en la carrera estudiamos esto mismo pero con esferas, en tres dimensiones, que es más complicado. tendría que repasármelo si quisiera hablar de ello...
ResponderEliminarinma, este post es un poco la continuación del que hice sobre el papel de burbujas. cuando apilas latas o cualquier objeto de forma cilíndrica, al cortar por un plano transversal, equivale al problema de las circunferencias tangentes entre sí. la retícula de circunferencias estructura triangular está en muchos sitios, ahora me estoy dando cuenta.
besos!
Buena clase teórica...a ver si soy capaz de llevarla a la práctica, jejeje.
ResponderEliminarBesosssss.
Hola Chema
ResponderEliminarTu blog es una caja de sorpresas dónde se puede encontrar cualquier cosa y eso lo hace tan especial...como creo que eres tú
Visitarte es volver con una sonrisa y cara de asombro a la vez
Me ha encantado el cuento de los gatitos
elanor, en este tipo de entradas suelo preparar primero los escaneados: los dibujitos y cálculos hechos a mano. y pienso: "lo más difícil ya está hecho, ahora escribir el texto es pan comido". pero luego cuando abro el documento de word en blanco y empiezo a escribir, no es tan fácil. tengo que pensar mucho cómo explicar las cosas para que se me entienda bien, jeje.
ResponderEliminarprincesa nadie, gracias por los halagos!! :) me dejo llevar, publico cosas que tengo en la mente en ese momento, sin etiquetar ni nada. como en un sueño, vamos pasando de unas cosas a otras sin conexión lógica, jeje. el próximo cuento que publicaré es el de los tres ositos, que ya lo tengo escaneado. pronto lo veréis!
besos
Déjate de consideraciones y abramos esas botellas... ¿De vino? así se acaba el problema de apilarlas, ja ja... Bss
ResponderEliminarYo estoy con Cari, jajajaja,¡a bebernos esas botellas! A mí las matemáticas no me van y contigo estoy aprendiendo incluso, jajajaja... Besos. ¡Y estás muy guapo pelado!
ResponderEliminarcari, es verdad, ves esa caja de botellas y dan ganas de abrir una! que además a mí me gusta descorchar botellas de champán, cuando hay una fiesta en casa suelo hacerlo yo. :D entra fácil, es como un refresco, pero luego te alegra, jejeje.
ResponderEliminarmerchi, quien ha visitado mi blog varias veces sabe que de vez en cuando hago este tipo de entradas, pero alguien que entre por primera vez y lo vea dirá "pero qué es estooo?" :D las mates es que hay que intentar explicarlas de forma amena y aplicándolas a cosas reales, jeje.
besos!
Así apilo yo mis botellas de agua de Solares, bueno, ellas tienden a apilarse así ellas solas.
ResponderEliminarMe alucina los posts que se te ocurren relacionados con tu matemanía. Eres único, Chemist!
Besos
rosana, así es, tienden a apilarse ellas mismas así porque es la configuración de mínima energía! :) por cierto, el agua solares ahora también la hacen con gas, en unas botellas verdes de cristal que me recuerdan a las de la marca perrier.
ResponderEliminarbesos!