
se me ha ocurrido que podía contaros algunas curiosidades sobre el movimiento de las agujas de los relojes... pronto nos van a cambiar la hora otra vez, pero las propiedades de dicho movimiento no se van a ver afectadas por el hecho de que sea una hora más tarde o más temprano. ;)
podemos estudiar el giro de las agujas dentro de un ciclo temporal de doce horas, de 12 en punto del mediodía a 12 en punto de la noche, o viceversa. sea como sea, a las 12 en punto empieza a contar el tiempo, luego la variable temporal t tomará el valor 0.
al ángulo recorrido por la aguja horaria lo llamaremos Φ (fi mayúscula). este ángulo nunca podrá ser mayor que una vuelta completa, pues hemos tomado como intervalo de estudio 12 horas. por otro lado, al ángulo barrido por la aguja minutera lo llamaremos φ (fi minúscula). esta aguja sí que da varias vueltas a la circunferencia a lo largo del ciclo de 12 horas -da 12 vueltas, de hecho-. ambos ángulos los mediremos en grados hexagesimales.
el ángulo recorrido por una aguja será igual a la velocidad angular de esa aguja multiplicada por el tiempo. para que las unidades sean coherentes, la velocidad se medirá en grados por minuto, y el tiempo en minutos. el resultado, que es el ángulo, se obtendrá en grados.
a la velocidad angular de la aguja horaria la llamaremos Ω (omega mayúscula). veamos cómo calculamos su valor. esta aguja pasa en el tiempo de 1 hora de un dígito del reloj al siguiente. qué ángulo separa dos dígitos consecutivos del reloj? será el ángulo completo dividido en 12 partes: 360º/12=30º. por tanto, recorre 30 grados en 60 minutos. si dividimos por 30 en el numerador y en el denominador de la fracción, obtenemos que recorre medio grado por minuto.
a la velocidad angular de la aguja minutera, por su parte, la llamaremos ω (omega minúscula). su valor será más sencillo de calcular. esta aguja da una vuelta completa a la circunferencia en 1 hora, luego recorre 360 grados en 60 minutos. dividiendo por 60 en el numerador y denominador de la fracción, obtenemos la cifra de 6 grados por minuto.
las agujas horaria y minutera inician su recorrido superpuestas una sobre la otra. a partir de ese instante, la minutera gira más rápido. en un momento dado estará en posición perpendicular a la horaria; después, estarán alineadas en sentidos opuestos; más tarde, la minutera volverá a estar perpendicular a la horaria, pero en posición opuesta según se mira la horaria desde su centro hasta su punta; y por último, la minutera alcanzará a la horaria y se volverán a superponer.
las horas exactas en las que se dan estas posiciones relativas de las agujas se obtienen calculando el ángulo que éstas forman entre sí. podemos restar el ángulo girado por la aguja horaria del ángulo girado por la aguja minutera -para que la diferencia tenga signo positivo, ya que el primero, que es el que se resta, es menor-.
el tiempo t se mide igual en las dos fórmulas, luego se puede sacar como factor común. se obtiene un coeficiente cuyo valor es la diferencia entre las dos velocidades angulares, es decir, 6-0.5=5.5. dicho coeficiente se mide en grados por minuto, y va multiplicado por el tiempo, que se mide en minutos.
a las 12 en punto las agujas están superpuestas. a las 3 en punto y a las 9 en punto están perpendiculares entre sí. a las 6 en punto están alineadas en sentidos opuestos. éstos son los casos más evidentes, y si al emplear la fórmula que hemos hallado los obtenemos como casos particulares, será señal de que lo estamos haciendo bien.
las horas exactas en las que se dan estas posiciones relativas de las agujas se obtienen calculando el ángulo que éstas forman entre sí. podemos restar el ángulo girado por la aguja horaria del ángulo girado por la aguja minutera -para que la diferencia tenga signo positivo, ya que el primero, que es el que se resta, es menor-.
el tiempo t se mide igual en las dos fórmulas, luego se puede sacar como factor común. se obtiene un coeficiente cuyo valor es la diferencia entre las dos velocidades angulares, es decir, 6-0.5=5.5. dicho coeficiente se mide en grados por minuto, y va multiplicado por el tiempo, que se mide en minutos.
a las 12 en punto las agujas están superpuestas. a las 3 en punto y a las 9 en punto están perpendiculares entre sí. a las 6 en punto están alineadas en sentidos opuestos. éstos son los casos más evidentes, y si al emplear la fórmula que hemos hallado los obtenemos como casos particulares, será señal de que lo estamos haciendo bien.
vamos a calcular, en primer lugar, las diferentes horas en las cuales las dos agujas se superponen. para ello, el ángulo que forman las agujas debe ser un múltiplo entero de vueltas completas, es decir, n*360º. se podría pensar que el ángulo que forman es de 0 grados, pero en realidad la aguja minutera, que es más rápida, ha superado a la horaria en n vueltas.
no nos preocuparemos del rango de valores que va a tomar n. simplemente le daremos valores hasta que volvamos al punto de donde habíamos partido, al comienzo del ciclo.
no nos preocuparemos del rango de valores que va a tomar n. simplemente le daremos valores hasta que volvamos al punto de donde habíamos partido, al comienzo del ciclo.
para n=0, el tiempo t es 0, estamos en el origen. cuál es nuestro origen? las 12 en punto. este primer resultado era previsible. efectivamente, a las 12 las agujas están superpuestas, como habíamos comentado.
ahora calculamos el valor que toma la fórmula para n=1. aclaro que, en adelante, el símbolo similar a un acento circunflejo (^) sobre un grupo de dígitos decimales, indica que esos dígitos se repiten periódicamente hasta el infinito.
hemos obtenido una cifra en minutos. veamos cómo se pasa a una hora del reloj expresada en horas, minutos y segundos. se hará igual en todos los casos.
al dividir esa cifra en minutos por 60, obtenemos el equivalente en horas. esa cifra en horas tendrá una parte entera y una parte decimal. la parte entera tomamos buena nota de ella, porque será el número de horas del tiempo que buscamos. ahora nos ocupamos de la parte decimal.
la parte decimal del tiempo expresado en horas, la multiplicaremos por 60 para pasarla a minutos. nuevamente el resultado tendrá una parte entera y una parte decimal. haremos algo análogo a lo hecho en el paso anterior. separamos la parte entera y nos quedamos con ella: será el número de minutos. a continuación, tomamos la parte decimal.
esa última parte decimal, cuyas unidades son minutos, si la multiplicamos por 60 la pasaremos a segundos. el resultado será el número de segundos definitivo, aunque tenga decimales, que los tendrá. no nos interesa llegar a unidades inferiores al segundo.
al dividir esa cifra en minutos por 60, obtenemos el equivalente en horas. esa cifra en horas tendrá una parte entera y una parte decimal. la parte entera tomamos buena nota de ella, porque será el número de horas del tiempo que buscamos. ahora nos ocupamos de la parte decimal.
la parte decimal del tiempo expresado en horas, la multiplicaremos por 60 para pasarla a minutos. nuevamente el resultado tendrá una parte entera y una parte decimal. haremos algo análogo a lo hecho en el paso anterior. separamos la parte entera y nos quedamos con ella: será el número de minutos. a continuación, tomamos la parte decimal.
esa última parte decimal, cuyas unidades son minutos, si la multiplicamos por 60 la pasaremos a segundos. el resultado será el número de segundos definitivo, aunque tenga decimales, que los tendrá. no nos interesa llegar a unidades inferiores al segundo.
así, para n=1, obtenemos la siguiente hora en la que las agujas están superpuestas, después de las 12 en punto.
seguimos dando valores a n y calculando las siguientes horas de forma análoga.






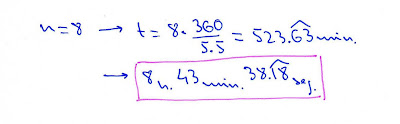


comprobamos que para n=11 hemos vuelto al punto de partida, las 12 en punto. se veía venir que se estaba cerrando el ciclo. ya no es necesario continuar.
pasamos ahora al caso en que las agujas se encuentran perpendiculares entre sí. para ello, vamos a exigir que el ángulo que forman sea un múltiplo impar del ángulo recto, un número impar de veces el ángulo de 90 grados. por qué impar? porque si incluyéramos los múltiplos pares de 90 grados, abarcaríamos el ángulo llano (180 grados) que es otro caso diferente que estudiaremos después; e incluso con los múltiplos pares de segundo grado de 90 abarcaríamos los casos de ángulo completo (360 grados) que son los de ambas agujas superpuestas que hemos analizado antes.
es decir, que nos interesan sólo los múltiplos impares. por decirlo de alguna manera, hay que tomar el primer ángulo recto, y a partir de ahí ir ‘a saltos’ para no coger por medio los ángulos llanos ni los ángulos completos. sólo nos interesan los rectos. los múltiplos impares de 90 grados los obtendremos multiplicando por 2*n+1 y dando valores a n a partir de n=0.
pasamos ahora al caso en que las agujas se encuentran perpendiculares entre sí. para ello, vamos a exigir que el ángulo que forman sea un múltiplo impar del ángulo recto, un número impar de veces el ángulo de 90 grados. por qué impar? porque si incluyéramos los múltiplos pares de 90 grados, abarcaríamos el ángulo llano (180 grados) que es otro caso diferente que estudiaremos después; e incluso con los múltiplos pares de segundo grado de 90 abarcaríamos los casos de ángulo completo (360 grados) que son los de ambas agujas superpuestas que hemos analizado antes.
es decir, que nos interesan sólo los múltiplos impares. por decirlo de alguna manera, hay que tomar el primer ángulo recto, y a partir de ahí ir ‘a saltos’ para no coger por medio los ángulos llanos ni los ángulos completos. sólo nos interesan los rectos. los múltiplos impares de 90 grados los obtendremos multiplicando por 2*n+1 y dando valores a n a partir de n=0.
comprobaremos que vamos a obtener más casos de agujas perpendiculares que de agujas superpuestas: exactamente el doble. esto se debe a que, mirando la aguja horaria desde el centro del reloj hasta la punta, la aguja minutera puede ser perpendicular con su punta mirando hacia un lado o hacia el lado opuesto.
una vez explicado esto, empezamos a dar valores a n. nos fijamos en la hora que calculemos para n=0, y cuando volvamos a obtener esa misma hora querrá decir que habremos cerrado el ciclo.
una vez explicado esto, empezamos a dar valores a n. nos fijamos en la hora que calculemos para n=0, y cuando volvamos a obtener esa misma hora querrá decir que habremos cerrado el ciclo.






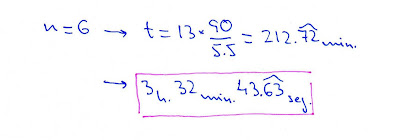















ésta es la misma hora que nos había salido para n=0, luego ya no hace falta continuar. entre las horas que hemos obtenido en las cuales las agujas son perpendiculares están las 3 en punto y las 9 en punto, como era previsible.
veamos el último caso particular de posiciones relativas de las agujas. esta vez calcularemos las horas para las cuales las agujas se encuentran alineadas en sentidos opuestos, es decir, formando un ángulo de 180 grados.
la condición que impondremos sobre el ángulo que forman las agujas es que sea un múltiplo impar de 180 grados. el motivo de que sea un múltiplo impar es evitar incluir los ángulos completos (360 grados), que corresponderían al caso de agujas superpuestas. es un razonamiento análogo al que hacíamos para el caso de las agujas perpendiculares.
el número impar se representa por 2*n+1 al igual que antes, y se van dando valores a partir de n=0. nos fijamos en la hora obtenida, y cuando nos vuelva a salir para otro valor de n posterior, ya no tendremos que continuar.
veamos el último caso particular de posiciones relativas de las agujas. esta vez calcularemos las horas para las cuales las agujas se encuentran alineadas en sentidos opuestos, es decir, formando un ángulo de 180 grados.
la condición que impondremos sobre el ángulo que forman las agujas es que sea un múltiplo impar de 180 grados. el motivo de que sea un múltiplo impar es evitar incluir los ángulos completos (360 grados), que corresponderían al caso de agujas superpuestas. es un razonamiento análogo al que hacíamos para el caso de las agujas perpendiculares.
el número impar se representa por 2*n+1 al igual que antes, y se van dando valores a partir de n=0. nos fijamos en la hora obtenida, y cuando nos vuelva a salir para otro valor de n posterior, ya no tendremos que continuar.











ésta es la primera hora en la cual las agujas están alineadas en sentidos opuestos. hemos vuelto al punto de partida. entre las horas obtenidas está la de las 6 en punto, como cabía esperar.
bueno, pues espero que esta entrada os haya gustado, y que a partir de ahora los relojes los veáis con otros ojos. ;) aunque me temo que con tanto cálculo, es muy posible que os hayáis dormido... si es así, el reloj de tintín, que marca las horas con campanadas, os despertará. :D
bueno, pues espero que esta entrada os haya gustado, y que a partir de ahora los relojes los veáis con otros ojos. ;) aunque me temo que con tanto cálculo, es muy posible que os hayáis dormido... si es así, el reloj de tintín, que marca las horas con campanadas, os despertará. :D












