
se me ha ocurrido que podía contaros algunas curiosidades sobre el movimiento de las agujas de los relojes... pronto nos van a cambiar la hora otra vez, pero las propiedades de dicho movimiento no se van a ver afectadas por el hecho de que sea una hora más tarde o más temprano. ;)
podemos estudiar el giro de las agujas dentro de un ciclo temporal de doce horas, de 12 en punto del mediodía a 12 en punto de la noche, o viceversa. sea como sea, a las 12 en punto empieza a contar el tiempo, luego la variable temporal t tomará el valor 0.
al ángulo recorrido por la aguja horaria lo llamaremos Φ (fi mayúscula). este ángulo nunca podrá ser mayor que una vuelta completa, pues hemos tomado como intervalo de estudio 12 horas. por otro lado, al ángulo barrido por la aguja minutera lo llamaremos φ (fi minúscula). esta aguja sí que da varias vueltas a la circunferencia a lo largo del ciclo de 12 horas -da 12 vueltas, de hecho-. ambos ángulos los mediremos en grados hexagesimales.
el ángulo recorrido por una aguja será igual a la velocidad angular de esa aguja multiplicada por el tiempo. para que las unidades sean coherentes, la velocidad se medirá en grados por minuto, y el tiempo en minutos. el resultado, que es el ángulo, se obtendrá en grados.
a la velocidad angular de la aguja horaria la llamaremos Ω (omega mayúscula). veamos cómo calculamos su valor. esta aguja pasa en el tiempo de 1 hora de un dígito del reloj al siguiente. qué ángulo separa dos dígitos consecutivos del reloj? será el ángulo completo dividido en 12 partes: 360º/12=30º. por tanto, recorre 30 grados en 60 minutos. si dividimos por 30 en el numerador y en el denominador de la fracción, obtenemos que recorre medio grado por minuto.
a la velocidad angular de la aguja minutera, por su parte, la llamaremos ω (omega minúscula). su valor será más sencillo de calcular. esta aguja da una vuelta completa a la circunferencia en 1 hora, luego recorre 360 grados en 60 minutos. dividiendo por 60 en el numerador y denominador de la fracción, obtenemos la cifra de 6 grados por minuto.
las agujas horaria y minutera inician su recorrido superpuestas una sobre la otra. a partir de ese instante, la minutera gira más rápido. en un momento dado estará en posición perpendicular a la horaria; después, estarán alineadas en sentidos opuestos; más tarde, la minutera volverá a estar perpendicular a la horaria, pero en posición opuesta según se mira la horaria desde su centro hasta su punta; y por último, la minutera alcanzará a la horaria y se volverán a superponer.
las horas exactas en las que se dan estas posiciones relativas de las agujas se obtienen calculando el ángulo que éstas forman entre sí. podemos restar el ángulo girado por la aguja horaria del ángulo girado por la aguja minutera -para que la diferencia tenga signo positivo, ya que el primero, que es el que se resta, es menor-.
el tiempo t se mide igual en las dos fórmulas, luego se puede sacar como factor común. se obtiene un coeficiente cuyo valor es la diferencia entre las dos velocidades angulares, es decir, 6-0.5=5.5. dicho coeficiente se mide en grados por minuto, y va multiplicado por el tiempo, que se mide en minutos.
a las 12 en punto las agujas están superpuestas. a las 3 en punto y a las 9 en punto están perpendiculares entre sí. a las 6 en punto están alineadas en sentidos opuestos. éstos son los casos más evidentes, y si al emplear la fórmula que hemos hallado los obtenemos como casos particulares, será señal de que lo estamos haciendo bien.
las horas exactas en las que se dan estas posiciones relativas de las agujas se obtienen calculando el ángulo que éstas forman entre sí. podemos restar el ángulo girado por la aguja horaria del ángulo girado por la aguja minutera -para que la diferencia tenga signo positivo, ya que el primero, que es el que se resta, es menor-.
el tiempo t se mide igual en las dos fórmulas, luego se puede sacar como factor común. se obtiene un coeficiente cuyo valor es la diferencia entre las dos velocidades angulares, es decir, 6-0.5=5.5. dicho coeficiente se mide en grados por minuto, y va multiplicado por el tiempo, que se mide en minutos.
a las 12 en punto las agujas están superpuestas. a las 3 en punto y a las 9 en punto están perpendiculares entre sí. a las 6 en punto están alineadas en sentidos opuestos. éstos son los casos más evidentes, y si al emplear la fórmula que hemos hallado los obtenemos como casos particulares, será señal de que lo estamos haciendo bien.
vamos a calcular, en primer lugar, las diferentes horas en las cuales las dos agujas se superponen. para ello, el ángulo que forman las agujas debe ser un múltiplo entero de vueltas completas, es decir, n*360º. se podría pensar que el ángulo que forman es de 0 grados, pero en realidad la aguja minutera, que es más rápida, ha superado a la horaria en n vueltas.
no nos preocuparemos del rango de valores que va a tomar n. simplemente le daremos valores hasta que volvamos al punto de donde habíamos partido, al comienzo del ciclo.
no nos preocuparemos del rango de valores que va a tomar n. simplemente le daremos valores hasta que volvamos al punto de donde habíamos partido, al comienzo del ciclo.
para n=0, el tiempo t es 0, estamos en el origen. cuál es nuestro origen? las 12 en punto. este primer resultado era previsible. efectivamente, a las 12 las agujas están superpuestas, como habíamos comentado.
ahora calculamos el valor que toma la fórmula para n=1. aclaro que, en adelante, el símbolo similar a un acento circunflejo (^) sobre un grupo de dígitos decimales, indica que esos dígitos se repiten periódicamente hasta el infinito.
hemos obtenido una cifra en minutos. veamos cómo se pasa a una hora del reloj expresada en horas, minutos y segundos. se hará igual en todos los casos.
al dividir esa cifra en minutos por 60, obtenemos el equivalente en horas. esa cifra en horas tendrá una parte entera y una parte decimal. la parte entera tomamos buena nota de ella, porque será el número de horas del tiempo que buscamos. ahora nos ocupamos de la parte decimal.
la parte decimal del tiempo expresado en horas, la multiplicaremos por 60 para pasarla a minutos. nuevamente el resultado tendrá una parte entera y una parte decimal. haremos algo análogo a lo hecho en el paso anterior. separamos la parte entera y nos quedamos con ella: será el número de minutos. a continuación, tomamos la parte decimal.
esa última parte decimal, cuyas unidades son minutos, si la multiplicamos por 60 la pasaremos a segundos. el resultado será el número de segundos definitivo, aunque tenga decimales, que los tendrá. no nos interesa llegar a unidades inferiores al segundo.
al dividir esa cifra en minutos por 60, obtenemos el equivalente en horas. esa cifra en horas tendrá una parte entera y una parte decimal. la parte entera tomamos buena nota de ella, porque será el número de horas del tiempo que buscamos. ahora nos ocupamos de la parte decimal.
la parte decimal del tiempo expresado en horas, la multiplicaremos por 60 para pasarla a minutos. nuevamente el resultado tendrá una parte entera y una parte decimal. haremos algo análogo a lo hecho en el paso anterior. separamos la parte entera y nos quedamos con ella: será el número de minutos. a continuación, tomamos la parte decimal.
esa última parte decimal, cuyas unidades son minutos, si la multiplicamos por 60 la pasaremos a segundos. el resultado será el número de segundos definitivo, aunque tenga decimales, que los tendrá. no nos interesa llegar a unidades inferiores al segundo.
así, para n=1, obtenemos la siguiente hora en la que las agujas están superpuestas, después de las 12 en punto.
seguimos dando valores a n y calculando las siguientes horas de forma análoga.






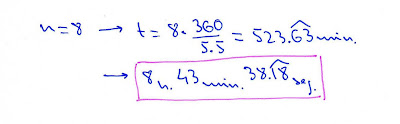


comprobamos que para n=11 hemos vuelto al punto de partida, las 12 en punto. se veía venir que se estaba cerrando el ciclo. ya no es necesario continuar.
pasamos ahora al caso en que las agujas se encuentran perpendiculares entre sí. para ello, vamos a exigir que el ángulo que forman sea un múltiplo impar del ángulo recto, un número impar de veces el ángulo de 90 grados. por qué impar? porque si incluyéramos los múltiplos pares de 90 grados, abarcaríamos el ángulo llano (180 grados) que es otro caso diferente que estudiaremos después; e incluso con los múltiplos pares de segundo grado de 90 abarcaríamos los casos de ángulo completo (360 grados) que son los de ambas agujas superpuestas que hemos analizado antes.
es decir, que nos interesan sólo los múltiplos impares. por decirlo de alguna manera, hay que tomar el primer ángulo recto, y a partir de ahí ir ‘a saltos’ para no coger por medio los ángulos llanos ni los ángulos completos. sólo nos interesan los rectos. los múltiplos impares de 90 grados los obtendremos multiplicando por 2*n+1 y dando valores a n a partir de n=0.
pasamos ahora al caso en que las agujas se encuentran perpendiculares entre sí. para ello, vamos a exigir que el ángulo que forman sea un múltiplo impar del ángulo recto, un número impar de veces el ángulo de 90 grados. por qué impar? porque si incluyéramos los múltiplos pares de 90 grados, abarcaríamos el ángulo llano (180 grados) que es otro caso diferente que estudiaremos después; e incluso con los múltiplos pares de segundo grado de 90 abarcaríamos los casos de ángulo completo (360 grados) que son los de ambas agujas superpuestas que hemos analizado antes.
es decir, que nos interesan sólo los múltiplos impares. por decirlo de alguna manera, hay que tomar el primer ángulo recto, y a partir de ahí ir ‘a saltos’ para no coger por medio los ángulos llanos ni los ángulos completos. sólo nos interesan los rectos. los múltiplos impares de 90 grados los obtendremos multiplicando por 2*n+1 y dando valores a n a partir de n=0.
comprobaremos que vamos a obtener más casos de agujas perpendiculares que de agujas superpuestas: exactamente el doble. esto se debe a que, mirando la aguja horaria desde el centro del reloj hasta la punta, la aguja minutera puede ser perpendicular con su punta mirando hacia un lado o hacia el lado opuesto.
una vez explicado esto, empezamos a dar valores a n. nos fijamos en la hora que calculemos para n=0, y cuando volvamos a obtener esa misma hora querrá decir que habremos cerrado el ciclo.
una vez explicado esto, empezamos a dar valores a n. nos fijamos en la hora que calculemos para n=0, y cuando volvamos a obtener esa misma hora querrá decir que habremos cerrado el ciclo.






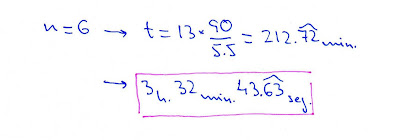















ésta es la misma hora que nos había salido para n=0, luego ya no hace falta continuar. entre las horas que hemos obtenido en las cuales las agujas son perpendiculares están las 3 en punto y las 9 en punto, como era previsible.
veamos el último caso particular de posiciones relativas de las agujas. esta vez calcularemos las horas para las cuales las agujas se encuentran alineadas en sentidos opuestos, es decir, formando un ángulo de 180 grados.
la condición que impondremos sobre el ángulo que forman las agujas es que sea un múltiplo impar de 180 grados. el motivo de que sea un múltiplo impar es evitar incluir los ángulos completos (360 grados), que corresponderían al caso de agujas superpuestas. es un razonamiento análogo al que hacíamos para el caso de las agujas perpendiculares.
el número impar se representa por 2*n+1 al igual que antes, y se van dando valores a partir de n=0. nos fijamos en la hora obtenida, y cuando nos vuelva a salir para otro valor de n posterior, ya no tendremos que continuar.
veamos el último caso particular de posiciones relativas de las agujas. esta vez calcularemos las horas para las cuales las agujas se encuentran alineadas en sentidos opuestos, es decir, formando un ángulo de 180 grados.
la condición que impondremos sobre el ángulo que forman las agujas es que sea un múltiplo impar de 180 grados. el motivo de que sea un múltiplo impar es evitar incluir los ángulos completos (360 grados), que corresponderían al caso de agujas superpuestas. es un razonamiento análogo al que hacíamos para el caso de las agujas perpendiculares.
el número impar se representa por 2*n+1 al igual que antes, y se van dando valores a partir de n=0. nos fijamos en la hora obtenida, y cuando nos vuelva a salir para otro valor de n posterior, ya no tendremos que continuar.











ésta es la primera hora en la cual las agujas están alineadas en sentidos opuestos. hemos vuelto al punto de partida. entre las horas obtenidas está la de las 6 en punto, como cabía esperar.
bueno, pues espero que esta entrada os haya gustado, y que a partir de ahora los relojes los veáis con otros ojos. ;) aunque me temo que con tanto cálculo, es muy posible que os hayáis dormido... si es así, el reloj de tintín, que marca las horas con campanadas, os despertará. :D
bueno, pues espero que esta entrada os haya gustado, y que a partir de ahora los relojes los veáis con otros ojos. ;) aunque me temo que con tanto cálculo, es muy posible que os hayáis dormido... si es así, el reloj de tintín, que marca las horas con campanadas, os despertará. :D













¡My god! una vez tuve una pesadilla, me perseguína los números. De nuevo un estupendo trabajo de cálculo pero indescifrable para mis ojos paganos jejjejej.
ResponderEliminarEn una csa si que me podrías ayuda, mañana cambian la hora pero no se si hay que adelantar o atrasar, ¿tu lo sabes?
Un beso Chema.
Pd: Milú está muy guapo :P
Me he perdido... Lo he intentado, conste, pero me perdí totalmente antes de la mitad. Ahora estoy enseñando a sumar a mi hijo y de momento la cosa va bien porque son sumas de una sola cifra hasta el diez. Cuando se complique más, te lo remito, vale?
ResponderEliminarLa hora se cambia esta madrugada, no? Creo que hay que atrasarlo, pero no estoy segura. Menudo rollo!!
Besos, Chema!
wendy, la verdad es que hasta yo, con lo que me gustan los números, he acabado cansado de tantos cálculos que he tenido que hacer para este post. ;) pero los números no son tan malos, jejeje. por cierto, hay muchas viñetas de tintín en las que milú puede pasar desapercibido, pero si te fijas sale poniendo unas caras muy graciosas.
ResponderEliminarblas, seguro que tu niño aprende sin problemas las sumas y todas las operaciones. pero si en algún momento se atasca, oye, sin problemas! me lo mandas a ver qué se puede hacer. ;) si has llegado a la mitad del post ya es mucho decir porque me ha salido larguísimo... :S
en cuanto a la hora, lo tengo que pensar siempre. se hará de noche antes. mañana, en vez de ser las 8 de la tarde, pongamos por caso, serán las 7. por tanto, habrá que... atrasar el reloj. hasta ese último paso tengo que pensarlo!
Menkanta este cambio y que por fin empiece el horario de invierno. A pesar de que no he sido capaz de leerme esta entrada, lo siento, Chema, lo del cambio horario lo domino. Esta noche tenemos que retrasar los relojes una hora, así que este fin de semana es el más largo del año. Por el contrario, el último sábado de marzo tendremos el cambio de primavera y el finde más corto.
ResponderEliminarMañana, a las seis de la tarde será de noche, podremos encender la chimenea, echarnos un riojita y asar almendras,mmmmmmmmm qué me gusta!!!!!!!
Bssssss
Cloti
Chema, Cloti, gracias por la explicación, aún no tenía claro que es lo que tenía que hacer esta noche con el reloj y por lo que veo Blas andaba igual de perdida jijjijijij.
ResponderEliminarBesos
Y los digitales, chema? ein? ein? y los digitales????
ResponderEliminarOops, lo siento Chema, pero ha sido ver la retahila de fórmulas y me ha entrado una pereza enoooorme.
ResponderEliminarConozco a alguien que mañana tiene un vuelo. Siempre me he preguntado si entre todos los que viajan en avión en días así habrá algún despistado que no sepa lo del cambio horario y pierda el vuelo...
Huy Anele, eso me pasó a mi en una ocasión.
ResponderEliminarEl vuelo salía a las 7 de la mañana y había que atrasar una hora el reloj, con lo cual el vuelo en realidad salía a las seis por mi reloj. No lo perdí por puñeter...ma casualidad.
Ostras Chema, esto ha sido demasiado para mi mente totalmente de letras. Lo siento, no he podido entender nada más que lo de Omegas y Phis. Ya después de eso me he perdido, mi mente se negaba a entender.....
ResponderEliminarLo que no puedo acabar de comprender es cómo se te pueden ocurrir estas cosas tan matemáticas al ver cosas para mí tan alejadas de las matemáticas!!!!! Qué mente tienes!
Besos!!
Oops, Blas. Mi teoría era cierta. Es que ¡corcho! es un riesgo tremendo. Si se te pasa lo del cambio horario la fastidias pero bien.
ResponderEliminarSobre todo imagínate que estás de vacaciones en el extranjero enfrascado en tus visitas y ni ves telediarios ni lees el periódico; fijo que no te enteras.
cloti, es verdad, es el fin de semana más largo del año. se dice que tenemos una hora más de sueño, pero en realidad es una hora más, para dormir o para lo que se quiera. y ahora ya sé que el otro cambio de hora es el último sábado de marzo. te sabes muy bien estos temas! visto así, no es tan malo que anochezca pronto. ;)
ResponderEliminarruth, con los digitales se podría hacer un estudio de cómo van moviéndose las líneas que forman los números. ;) cuando era pequeño fuimos de viaje en coche cama no recuerdo a dónde, y no me dormía ni a tiros. tenía mi reloj digital delante, y llegué a verlo marcar las 3 de la madrugada, 03:00.
anele, lo de las diferencias horarias es un lío. me ha venido a la mente lo que le ocurría al protagonista de 'la vuelta al mundo en 80 días', que era para bien. por cierto, hace poco me he enterado de que hay una isla de oceanía que se llama kiribati que es el lugar más oriental del mundo tal como está situada la línea de cambio de fecha, y por tanto es donde antes comienza el día.
rosana, la idea de esta entrada en principio me parecía que era sencilla, calcular las horas a las que las agujas "se pillan" una a la otra y a las que forman determinados ángulos. pero luego el desarrollo es larguííísimo, reconozco que me dejó exhausto, jejeje. luego intenté darle un poco de color con las imágenes de esther y de tintín. ;)
Vaya análisis horario!!Cuánto tienes que saber , para hacer un análisis matemático de cualquier cosa.Vaya maravilla de cabeza la tuya!
ResponderEliminarYo he intentado entenderlo.....pero nada.
Incapaz del todo. Vamos, que ni lo he intentado que una es de eltras y conoce sus limitaciones. Eso sí, me sigue admirando ver cómo ves matemáticas en todo lo que te rodea. Serás un profesor estupendo pues tus alumnos verán las matemáticas aplicadas a cosas reales y no al problema del libro.
ResponderEliminarImposible leerte entero. No me aclaro con las operaciones matemáticas.
ResponderEliminar¿Cómo sabes tú tanto de esto?
olatz, mientras escribía esta entrada estaba pensando que era muy 'analítica'. todo se resuelve con ecuaciones y cálculos. tengo en mente otra entrada para dentro de poco que será más 'gráfica', se hará todo con regla, escuadra, cartabón y compás sin realizar ningún cálculo ni medición. ésa te gustará más, es más de tu campo. :)
ResponderEliminarsusana, eso es verdad. las matemáticas y la física están en la vida real, y además en sus casos más formalmente más sencillos. en los relojes, por ejemplo, se trata de giros con velocidad constante, no de supuestos 'de laboratorio' extraños que a veces se encuentran en los problemas de los libros. hay que hacer hincapié en enseñar bien lo más sencillo, porque es lo que se encuentra en la realidad. gracias por los buenos augurios, espero verme de profe algún día!! ;)
inma, han sido muchos años viendo numeros y símbolos de estos, jejeje. se me ha quedado grabado a fuego que la serie de números pares es 2*n y la de impares 2*n+1, por ejemplo... y la mitad de las letras del alfabeto griego las hemos llegado a utilizar para unas cosas y otras! :D
jo, Chema, de verdad no sabes la fórmula de convertir el plomo en oro o algo así????
ResponderEliminarcoilet, es una buena idea, con eso nos podemos hacer ricos!! dónde está guardado el quimicefa de mi hermana?? :D
ResponderEliminar