mi amiga geno me regaló este libro sobre la proporción
áurea. no sé cómo pudo imaginarse que me gustaban estos temas, pero acertó
plenamente. ;)
hace tiempo publiqué en este blog tres entradas relacionadas
con el número áureo: la primera era sobre los pentágonos, la segunda sobre la
sucesión de fibonacci, y la tercera sobre las espirales.
leyendo el libro de national geographic, he aprendido
algunas cosas que no sabía...
veis este bucle infinito de fracciones? si se lo pongo a alguno
de mis alumn@s, pensará que he perdido el juicio.
si hacemos el inverso de este mamotreto, nos damos cuenta de
que es igual a la serie original -a la que llamamos x- menos una unidad.
desarrollando la ecuación, obtenemos que x no es otra cosa que el número áureo,
al que se suele denotar con la letra griega Φ.
y qué os parece esta serie infinita de raíces? da miedo, y casi
ningún adulto se acuerda de cómo se resolvían las raíces cuadradas...
si elevamos al cuadrado este engendro, observamos que es
igual al original más una unidad. eso nos conduce de nuevo a la ecuación de
segundo grado cuya solución es el número áureo.
otro concepto que he aprendido es el de gnomon. se denomina gnomon
de una figura geométrica a aquélla que yuxtapuesta a la primera nos dará
una nueva figura de la misma forma y proporciones que la original.
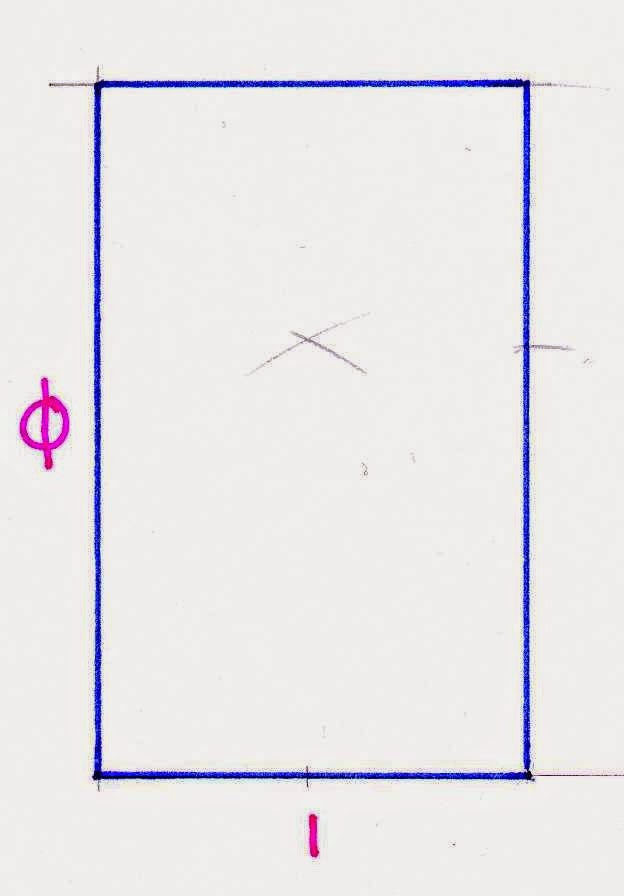
con ejemplos se verá más claro. aquí tenemos un rectángulo
áureo, cuyos lados miden 1 y Φ. la proporción entre el mayor y el menor es Φ,
la proporción áurea.
si le añadimos un cuadrado cuyo lado sea de longitud Φ -el lado
mayor del rectángulo original-, obtendremos un nuevo rectángulo áureo de
mayor tamaño que el primero.
veamos ahora el triángulo áureo, que es como se denomina al
triángulo isósceles formado por un lado de un pentágono regular y dos de sus
diagonales. su ángulo más cerrado es de 36º, y los más abiertos son de 72º.
pensemos ahora en otro importante triángulo isósceles, el
formado por dos lados del pentágono y una de las diagonales. tiene un ángulo obtuso
de 108º y dos ángulos agudos de 36º.
si tomamos un triángulo de este tipo cuyos lados iguales
tengan la misma longitud que los lados iguales del triángulo áureo del que
hablábamos, y lo unimos al primero como se indica en la figura, obtendremos un
nuevo triángulo áureo. así pues, el segundo triángulo es el gnomon del primero.
y a todo esto, vaya palabra, gnomon. no era así como se llamaba a una especie de enanitos que
vivían en el bosque...? ;)









Hola. ya veo que Geno acertó plenamente con el regalo del libro y aún aprendiste algo más!! Admiro a la gente como tu que teneis capacidad para los números... Muy interesante a cómo se llega desde los ángulos a la figura del gnomo. Es increíble!, seguimos en contacto
ResponderEliminarLo único que he entendido de todo el post ha sido David el Gnomo jajajajaja qué ignorante me siento, Chema de mi alma :D
ResponderEliminar25+5
Me alegro que te haya gustado. Realmente no fui yo la que acerté fue el libro el que se comunicó de alguna manera, le miré y dije "pa Chema" jajajajjaja
ResponderEliminar¿Por qué será? XDDD, creo que Geno tenía fácil qué tipo de libro elegir... Feliz fin de semana
ResponderEliminarmarta, lo de mezclar cálculos matemáticos con dibujitos chorras es una cosa muy típica mía, jeje. y aunque no lo he dicho, el triángulo áureo, con esa forma alta y estrecha, se parece un poco al gorro de un gnomo. ;)
ResponderEliminareva, no te preocupes, es que en esta entrada no he explicado las cosas de manera muy exhaustiva para no extenderme mucho, jeje. quería principalmente agradecerle a geno el regalo y hacer la gracieta del gnomo. :D
geno, al hilo de lo que dices, hay veces que los libros nos llaman. cuando echo un vistazo a un libro y no me decido a comprarlo, y al cabo de un tiempo considerable me lo vuelvo a encontrar, me parece como una señal, una segunda oportunidad que el destino me da para hacerme con él y leerlo. :D
lucía, así es, ese libro estaba en los kioscos, geno vio lo del número áureo, con la ilustración de la caracola con forma de espiral, y pensó en mí. qué fama tengo!! :D
¡Yo también me quedo con el gnomo!
ResponderEliminarComo te puedes acordar tan bien de todo eso,,,ahora que lo dices yo también lo recuerdo...fue en el blog de Wendy...¡Como la echo de menos!ojalá vuelva algún día cuando su trabajo se lo permita
Un Beso
¿No sabías lo que era el gnomon? jua, jua, habló la de letras. Me encanta que te entusiasmes tanto con las cosas que te gustan.
ResponderEliminarA mi también me gustaba calcular gráficamente la proporción áurea y buscarla en cuadros es super interesante :)
ResponderEliminarUn besazo guapo
princesa, así es. recuerdo todas vuestras primeras apariciones, jeje. a wendy tuve la suerte de conocerla en una miniquedada en murcia. la tengo en facebook, así que eso me sirve para seguirle un poco la pista.
ResponderEliminarses, la parte del gnomon la leí en la peluquería, mientras esperaba. lo busqué en google, y tiene su artículo de wikipedia y todo. es una palabra griega, creo recordar... tú estudiaste griego por haber elegido la rama de letras, pues mira, eso que te llevaste, es cultura.
queca, en los dibujos escaneados hay líneas y arcos auxiliares a lápiz que no quise borrar para darles más autenticidad, y son las que hice para sacar gráficamente la proporción áurea del lado base, jeje. y sí, en ese libro habla de cómo en muchas pinturas famosas se ha empleado la proporción áurea. como licenciada en bellas artes que eres, lo sabrás bien. :)
besos!!
Ufff...qué locura...creo que mi cerebro ha cortocircuitado. Recuerdo ver apuntes de mi hermano al respecto y pensar que era un tema muy bonito, pero muy difícil de entener para mí.
ResponderEliminarBesos!
fashion lover, lo del número áureo es un tema muy bonito, se habla de ello en todos los libros de matemáticas divulgativas. pero, al menos en mi caso, en el colegio muy poco (sólo en dibujo técnico de cou, de pasada), y en mi universidad cero patatero (y eso sí que tiene delito). en realidad se le podría explicar a cualquier niño, los únicos conocimientos previos que se requieren son el teorema de pitágoras y las ecuaciones de segundo grado. pero claro, bastante tienen con lo que les mandan estudiar en el colegio...
ResponderEliminar